近日，清华大学低维量子物理国家重点实验室成员、高等研究院教授姚宏及其研究组博士生简少恺和博士后阴帅在费米子体系三临界点的理论研究方面取得进展。

三临界点(tricritical point)是多体系统中一级相变和二级相变的分水岭。三临界点及其性质一直是凝聚态和统计物理中引起广泛关注的基本问题之一。二级相变点通常需要调控一个参数来实现，但需要调控两个参数才有可能实现三临界点，因此三临界点可以有更加丰富和有趣的性质。三临界点的研究吸引了实验、理论、和数值模拟的广泛兴趣。

研究表明，无质量的狄拉克费米子和序参量(波色场)之间的耦合可以定性地改变体系的临界特性，产生手征临界点。特别是，姚宏和简少恺及合作者们在2017年发现无质量的狄拉克费米子可以将原来玻色场的一级相变诱导为二级相变，这就是费米子诱导的临界性[Nature Communications 8, 314 (2017)]。但是，丰富多彩的三临界点和无质量狄拉克费米子的耦合对临界特性的定性影响还少有研究。

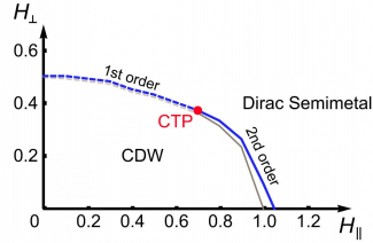
最近，姚宏教授研究组对此问题进行了理论研究。他们考虑蜂窝格子上的具有三临界点的自旋模型，并将其耦合于无质量狄拉克费米子场。他们发现在狄拉克半金属到绝缘体相变的边界上，存在一个新型的三临界点。通过平均场和泛函重整化群计算，他们发现此三临界点附近的临界行为定性地不同于通常玻色场的三临界性和手征临界性，而是形成一个新的三临界点普适类，并将其命名为“手征三临界点”(chiral tricritical point)，见下图。他们还进一步讨论了其可能的实验实现方案。

该研究成果以“Chiral Tricritical Point: A New Universality Class in Dirac Systems”为题，于2018年5月25日发表于《物理评论快报》杂志[Phys. Rev. Lett. 120, 215702 (2018)]。论文的通讯作者为姚宏教授和博士生简少恺，第一作者为高等研究院博士后阴帅。该研究工作得到了低维量子物理国家重点实验室自主科研基金、国家重点研发计划项目“二维新型量子体系的设计、调控和原型器件探索”和国家自然科学基金的支持。

文章全文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.120.215702