⾼温超导现象自从被发现以来,⼀直是凝聚态物理学中最重要最有挑战性的问题之⼀。人们普遍认为各种铜氧化物高温超导材料具有统一的相图特征,例如在半满填充的基础上掺杂空穴,系统基态会发生从反铁磁Mott绝缘体到超导体的转变。但形成高温超导的微观机制众说纷纭,至今仍未达成广泛共识。
近年来,清华物理系王亚愚研究组利用扫描隧道显微镜(STM)在欠掺杂的Ca2CuO2Cl2材料中观测到丰富的空穴局域态密度(LDOS)分布结构,呈现四叶草状、条纹状、阶梯状等图样 [arXiv:2309.09260],被认为是理解超导微观起源的关键线索。四叶草状的LDOS可视为Mott绝缘体中的“原子轨道”,而条纹状和阶梯状的LDOS可分别视为Mott绝缘体中的成键和反键“分子轨道”。然而,上述定性理解主要基于单粒子图像,而系统本身是强关联量子多体系统。因此有必要从微观模型出发,通过精确的多体计算,更好地理解这些特征分布的形成机制。此外,传统的理论计算主要基于Hubbard模型、t-J模型等格点模型,而STM测量的LDOS在连续实空间,与格点模型的基态电荷分布不便直接比较。因此需要设法建立理论、数值和实验的直接联系。
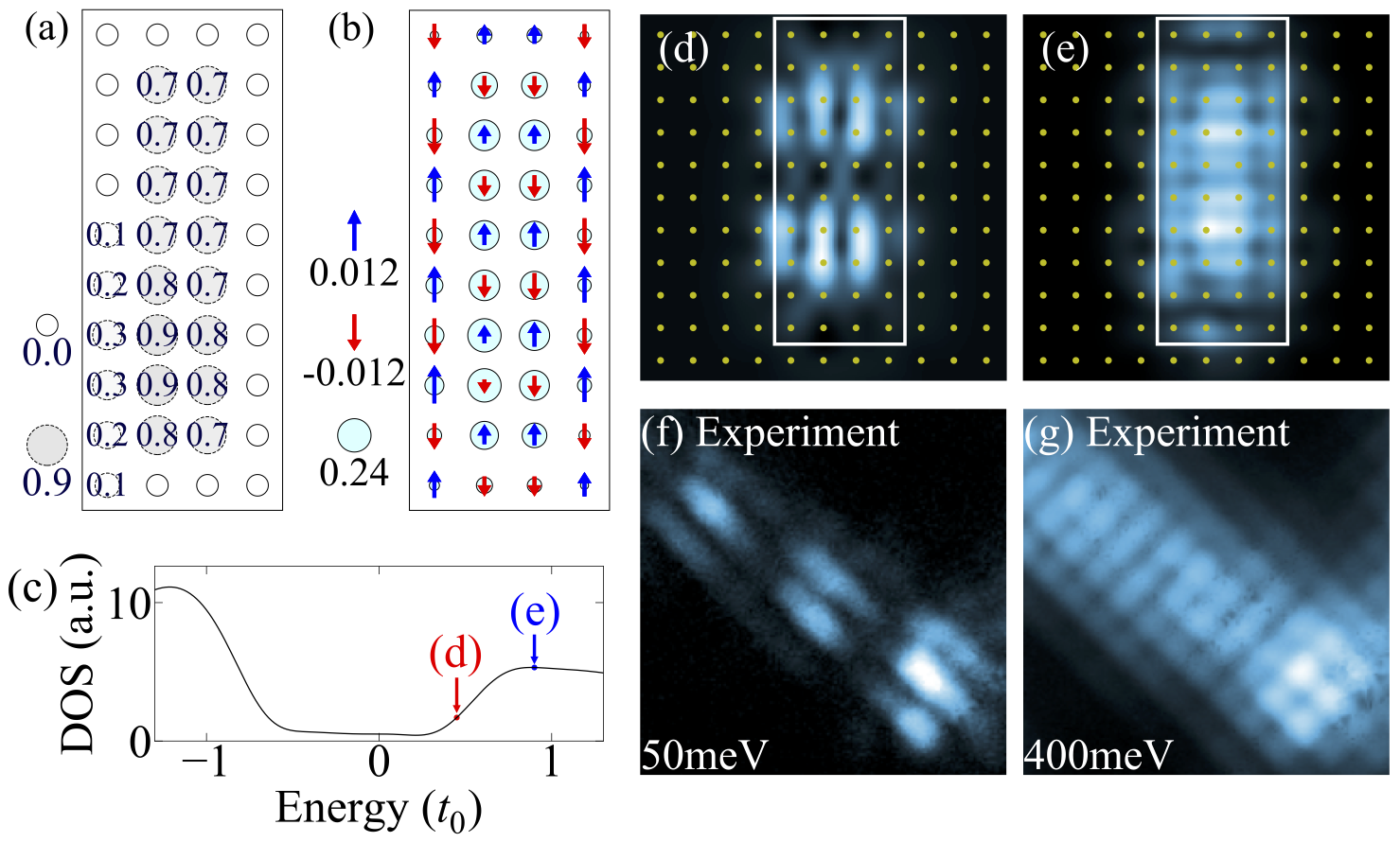
图1: Hubbard模型在半满基础上掺杂四个空穴时理论计算和实验观测的比较。(a) 10x4团簇上的杂质势场。(b) 基态的空穴密度和磁矩分布。(c) 四空穴情况的态密度。(d-e) 图(c)中箭头处能量对应的局域态密度。(f-g) 实验上在较低能量(f)和较高能量(g)测得的局域态密度,实验数据来自王亚愚研究组[arXiv:2309.09260]。理论计算和实验观测符合很好。
最近,清华物理系杨硕研究组针对上述问题开展了系统研究。首先,在Hubbard模型的基础上引入局域杂质势场来模拟实际材料中掺杂的影响(图1(a)),采用此前开发的切比雪夫矩阵乘积态方法,精确高效地计算出格点模型上的格林函数。然后,通过四叶草状的Wannier函数进行基矢变换,将格林函数映射至连续实空间,实现了和STM实验数据的直接比较(图1)。通过系统研究不同掺杂下的Hubbard模型,展示了杂质势场调控电荷有序态的演化规律。理论计算结果与实验观测符合很好(图1(d-g)),成功揭示了铜氧化物高温超导体中条纹-梯子状电荷调制结构的微观机制。
本研究为掺杂Mott绝缘体中的分子轨道理论提供了严格数值验证,揭示了棋盘格相与条纹相的内在联系,也证实了系统基态具有早期理论预言的条纹序。研究成果为高温超导微观机理的研究带来了新的见解,为理解超导涨落与电荷有序的关系提供了新的视角,所发展的连续空间映射方法架起了数值与实验的关键桥梁,也可直接推广至其他量子材料体系。
该研究成果以“Unveiling Stripe-Shaped Charge Density Modulations in Doped Mott Insulators”为题,于2025年9月11日发表在《物理评论快报》(Physical Review Letters)上。清华物理系博士生夏宁为本文的第一作者,物理系副教授杨硕为本文的通讯作者,论文工作参与者还包括物理系博士生郭雨尘。
此工作得到了国家自然科学基金、清华大学低维量子物理全国重点实验室、量子信息前沿科学中心、合肥实验室项目、清华大学笃实专项的支持。
文章链接:https://doi.org/10.1103/hmqb-9q91